Yesterday was the announcement of the Nobel Prize in Physics 2016 being awarded to David Thouless, Michael Kosterlitz and Duncan Haldane. Since the topic is very close to my own research, this is an excellent opportunity to revive this long-lost weblog. Another reason is that the award is essentially a recognition of the importance of topology in modern physics, but this relevance is hard to convey to the layman. Many reports I’ve seen failed badly, including these mystifying statements by a surely overwhelmed Haldane himself, and now it’s my turn to fall short in clarity.
Topology
So let’s start with what topology is, in the context of physics. Let’s say you have a piece of material and you want to describe to me some of its properties. For many of such properties, like color, mass density, crystal structure, electric resistivity etc. it doesn’t matter if you’re only looking at a small piece of the material—you can break it in pieces in any way you like, and each of the pieces will still give you the same, correct information. It turns out that there are some properties which rely on the object as a whole. Zooming in on any part of the object does not lead to any conclusive answer. The example given in the popular science memo about this Nobel Prize (pdf) is very good: if you give me a doughnut and ask me how many holes it has, I cannot answer by examing a single bite, I must look at the doughnut as a whole. It follows that small changes in the object do not affect these properties: each doughnut I bake looks slightly different, but they all have exactly one hole. This is called topological protection: these quantities can only be changed by changing the object as a whole, like slicing open the doughnut.
Ordered states and phase transitions
A large part of so-called condensed matter physics concerns the classification and characterization of different phases of matter. In school everybody learns about the phases of solid, liquid and gas (for instance ice, water and steam), but to a physicist being, for example, conductive or insulating are regarded as different phases of matter. Furthermore there are superfluids, superconductors, all kinds of magnets, plasmas etc. etc. The abrupt change between two phases is called a phase transition.
So now we want a measure to distinguish different phases from each other. Any quantity that can do this for you is called an order parameter. For instance, in a magnet the order parameter is the size and the direction of the magnetic field, whereas in a non-magnetic material, the magnetic field is zero. This is always the case: a good order parameter is zero in the less ordered state and non-zero in the more ordered state on the respective sides of the phase transition. For a solid, the order parameter captures the regular spacing between atoms while in the disordered liquid that quantity averages out to zero due to the essentially random positions of the atoms. Take this picture as an example:
 Here the phase is characterized by arrows that all point in the same direction. Being ordered means that if I know the orientation of one arrow, I know the orientation of all of them. Notice that I can only look at a part of this picture to determine in which direction the order has been established. This is therefore not topological order.
Here the phase is characterized by arrows that all point in the same direction. Being ordered means that if I know the orientation of one arrow, I know the orientation of all of them. Notice that I can only look at a part of this picture to determine in which direction the order has been established. This is therefore not topological order.
Topological defects
Of course, the order in a material is never perfect. There are always contaminations and impurities, and these may affect the particular value of the order parameter to some extent. For instance, the resistance of an electric conductor (a metal like copper) increases if the material is less pure. But it is still in the conducting phase. Furthermore such impurities are always local, which means they are small and only affect a limited region of the material.
In contrast, there are also entities that reduce the order parameter that are not local, and essentially extend throughout the whole material. Take a look at the following picture:

Using the same arrows as above, there is now a configuration where the arrows winding around a central point. Such a configuration is called a vortex. There are several things to note here:
- Far away from the center, nearby arrows point in almost the same direction. I can therefore not look at some small region to determine whether or not the vortex is present: it is a non-local entity.
- In the center of the vortex, the arrow cannot be chosen to point in any direction. This is called a singularity.
- Following the red line, the arrows wind precisely 360 degrees to come back to the original direction. One can only make vortices with multiples of 360 degrees and nothing in between. This is precisely a like the number of holes in a doughnut, which can be 0,1,2,… but not 0.83433.
- It does not matter where I draw the red line; it can be wavy, go out to the edge and back, whatever. As long as the line is closed (does not have endpoints) the arrows along the line always wind by 360 degrees. Therefore this winding is a topological quantity. It does not depend on local details and it cannot be modified unless all of the arrows are suddenly changed at the same time.
- Arrows that are far away now point in very different directions, meaning that the order of the previous picture is disturbed.
Because of 5. the vortex is an example of a defect in the ordered phase, and because of 4. it is called a topological defect. Topological defects are the subject of almost all my own research up to the present day. The project I am funded by at Keio University is actually called “Topological Science”.
Low-dimensional order
We are almost ready to talk about the Nobel Prize, there is one more piece of historical context necessary. Looking at the first picture, one would guess that ordered phases can exist in a two-dimensional plane as is drawn there, just as it would in real three-dimensional material. Even arrows that live on a line (one-dimensional) could all point in the same direction and be ordered.
Systems with dimension lower than three (so lines and planes) are called low dimensional. Even though everything in reality is three dimensional, one could imagine sheets of matter of one atom layer thick. In physics, even systems of several or several tens or hundreds atoms thick are said to be quasi two-dimensional, which means that they can be very well described by a two-dimensional model. Another important case is the interface between two materials.
So from the early days physicists have wondered about the properties of such low-dimensional systems, with surprising theoretical results. In the 1930s Rudolf Peierls had calculated that sound waves in a two-dimensional solid would be so violent as to prevent the formation of such a solid at all. Random sound waves are always present due to thermal excitation; it is the random motion of atoms in ordered state, let’s say the Brownian motion in solids. But now it turns out that the sound waves are much more pronounced as the dimension of a material gets lower. In the years 1966-1968 Mermin & Wagner, and Hohenberg wrote several articles that showed that this phenomenon is completely general and holds for any order and any phase of matter. The mathematical argument was so elementary that at the time no one doubted that ordered states are not possible in dimensions lower than three. So at the time every physicist was convinced that it is not even worth looking for any sort of order in two-dimensional systems.
Kosterlitz–Thouless phase transition
Every physicist? No, two brave researchers in Birmingham at the time, Kosterlitz and Thouless (and independently and earlier but less exhaustive Berezhinksii in Moscow) kept wondering about models that look like the first picture. The smart thing they did was not to look at what happens to the order parameter (first picture) itself, but what happens to the vortices (second picture). See, if you combine a winding of 360 degrees (vortex) with one of -360 (antivortex), that is, one clockwise and one counter-clockwise, the total configuration has again zero winding. The perturbance of the order due to a vortex–antivortex pair is therefore limited and local. See this picture:
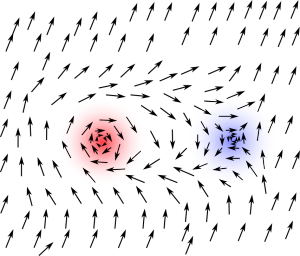
The arrows at the edge all point in the same direction and, apart from the region in the center, order is maintained. We can now look at the order–disorder phase transition from the point of view of the vortices. This is illustrated by this figure, which features on the cover of my PhD thesis.
The leftmost panel depicts the completely ordered state at low temperature while the rightmost one depicts the the completely disordered state at high temperature. The second panel shows one vortex–antivortex pair which is still a local excitation. The third panel features a few of such pairs. In terms of the arrows, their direction randomizes going left to right, but in terms of the vortices, they become more and more present. This is called vortex unbinding. In the final panel, vortices are no longer bound in pairs with antivortices but can exist freely. Therefore the phase transition from ordered to disordered can be viewed as a vortex-unbinding transition. In physics this is backed up by robust calculations.
The insight of Kosterlitz and Thouless was to start in the disordered state, which must surely be of the unbound vortices type, the rightmost panel. They then asked: what happens to these vortices if one lowers the temperature? And indeed, they found that the vortices at low temperature bind in pairs, even in two dimensions. They explicitly showed there was some ordering phase transition, but the earlier-mentioned theorems precluded the formation of a truly ordered phase. Therefore they discovered, theoretically, a new phase of matter. The interesting thing is that, even though it is surely more ordered than a completely disordered state, it is impossible to find a local order parameter like one can for ordinary phases. Instead, when zooming in the state looks just as in the left panel, but zooming out the direction of the arrows varies greatly. This goes under the name, which you can and should immediately forget, of algebraic long-range order.
The existence of such phases in two-dimensions has now been verified by many calculations and also in several experiments. So this special type of phase, which is neither disordered nor truly ordered, is actually found in nature.
Each type of order has its own type of topological defects, which presumably can undergo a similar unbinding transition. I have looked at this for vortices in superfluids and superconductors, and for topological defects in crystalline order. In the latter case, a solid can disorder into various stages of liquid crystals to finally disorder into a liquid. This is the topic of our most recent paper.
Topological phases
This Nobel Prize awards two more or less separate advances, the first being the Kosterlitz–Thouless phase transition, and the second what I’ll discuss now. Thouless played an important role here as well, so that half of the Prize has been awarded to him while the other two receive one quarter. This topic concerns an even more obscure concept, topological phases of matter. Since this post has gotten way too long already, I won’t say too much about it.
As before, this is about the characterization of phases of matter that don’t allow for any ordinary order parameter. Instead, there are distinct numbers, like the numbers of holes in a doughnut, that capture global properties of the object as a whole. The first instance of this is the quantum Hall effect discovered in 1980, which I won’t explain here. Thouless with collaborators showed that this phase of matter can indeed be characterized by a topological number, which does not depend on the local details of the material.
Duncan Haldane is this type of very original thinker that has contributed pioneering ideas to many parts of condensed matter physics. In this case he proposed a model which has surprising properties that would be unbelievable (as they were for quite a while) were it not for robust topological arguments. This model has actually been verified in experiment by now. Furthermore it was the inspiration for a new field of physics that is not even 10 years old, called topological insulators. This is a super-hot topic currently, due to its propensity to be captured by straightforward calculations that can by now be readily put to the test in experiment.
Lorentz chair
On a personal note, the Institute-Lorentz for theoretical physics at Leiden University, where I did my PhD, has an annual visiting professor, called the Lorentz chair, which has boasted many famous names over the years. In the hallway there is a gallery of portraits of Lorentz professors who also, usually subsequently, won the Nobel Prize. I am sure they are very happy to add one more, as Haldane was Lorentz professor in 2008, when I was there. I remember his lectures were both awe-inspiring and rather impenetrable, as they tend to be.

Wauw, goed zeg!
Ik heb het een stukje gelezen en denk dat ik het aardig kan lezen; over begrijpen zal ik het nog niet hebben 🙂 Ik zal er heel binnenkort goed voor gaan zitten.
When I heard about the Noble Prize I immediately thought of you and about asking you about this. I could follow your explanation rather well though I skipped some details. On the side: RSS rules.
Hi Aron
Nicely written blog!
Found it when googling for nice sketches of vortex-antivortex pairs.
ATB
Henrik