Nobel Prize in Physics 2016

Oct 052016
 
 5th October 2016 21:54JST  , , , , ,  3 Responses »

Yesterday was the announcement of the Nobel Prize in Physics 2016 being awarded to David Thouless, Michael Kosterlitz and Duncan Haldane. Since the topic is very close to my own research, this is an excellent opportunity to revive this long-lost weblog. Another reason is that the award is essentially a recognition of the importance of topology in modern physics, but this relevance is hard to convey to the layman. Many reports I’ve seen failed badly, including these mystifying statements by a surely overwhelmed Haldane himself, and now it’s my turn to fall short in clarity.

Topology

So let’s start with what topology is, in the context of physics. Let’s say you have a piece of material and you want to describe to me some of its properties. For many of such properties, like color, mass density, crystal structure, electric resistivity etc. it doesn’t matter if you’re only looking at a small piece of the material—you can break it in pieces in any way you like, and each of the pieces will still give you the same, correct  information. It turns out that there are some properties which rely on the object as a whole. Zooming in on any part of the object does not lead to any conclusive answer. The example given in the popular science memo about this Nobel Prize (pdf) is very good: if you give me a doughnut and ask me how many holes it has, I cannot answer by examing a single bite, I must look at the doughnut as a whole. It follows that small changes in the object do not affect these properties: each doughnut I bake looks slightly different, but they all have exactly one hole. This is called topological protection: these quantities can only be changed by changing the object as a whole, like slicing open the doughnut.

Ordered states and phase transitions

A large part of so-called condensed matter physics concerns the classification and characterization of different phases of matter. In school everybody learns about the phases of solid, liquid and gas (for instance ice, water and steam), but to a physicist being, for example, conductive or insulating are regarded as different phases of matter. Furthermore there are superfluids, superconductors, all kinds of magnets, plasmas etc. etc. The abrupt change between two phases is called a phase transition.

So now we want a measure to distinguish different phases from each other. Any quantity that can do this for you is called an order parameter. For instance, in a magnet the order parameter is the size and the direction of the magnetic field, whereas in a non-magnetic material, the magnetic field is zero. This is always the case: a good order parameter is zero in the less ordered state and non-zero in the more ordered state on the respective sides of the phase transition. For a solid, the order parameter captures the regular spacing between atoms while in the disordered liquid that quantity averages out to zero due to the essentially random positions of the atoms. Take this picture as an example:

ordered stateHere the phase is characterized by arrows that all point in the same direction. Being ordered means that if I know the orientation of one arrow, I know the orientation of all of them. Notice that I can only look at a part of this picture to determine in which direction the order has been established. This is therefore not topological order.

Topological defects

Of course, the order in a material is never perfect. There are always contaminations and impurities, and these may affect the particular value of the order parameter to some extent. For instance, the resistance of an electric conductor (a metal like copper) increases if the material is less pure. But it is still in the conducting phase. Furthermore such impurities are always local, which means they are small and only affect a limited region of the material.

In contrast, there are also entities that reduce the order parameter that are not local, and essentially extend throughout the whole material. Take a look at the following picture:

vortex

Using the same arrows as above, there is now a configuration where the arrows winding around a central point. Such a configuration is called a vortex. There are several things to note here:

  1. Far away from the center, nearby arrows point in almost the same direction. I can therefore not look at some small region to determine whether or not the vortex is present: it is a non-local entity.
  2. In the center of the vortex, the arrow cannot be chosen to point in any direction. This is called a singularity.
  3. Following the red line, the arrows wind precisely 360 degrees to come back to the original direction. One can only make vortices with multiples of 360 degrees and nothing in between. This is precisely a like the number of holes in a doughnut, which can be 0,1,2,… but not 0.83433.
  4. It does not matter where I draw the red line; it can be wavy, go out to the edge and back, whatever. As long as the line is closed (does not have endpoints) the arrows along the line always wind by 360 degrees. Therefore this winding is a topological quantity. It does not depend on local details and it cannot be modified unless all of the arrows are suddenly changed at the same time.
  5. Arrows that are far away now point in very different directions, meaning that the order of the previous picture is disturbed.

Because of 5. the vortex is an example of a defect in the ordered phase, and because of 4. it is called a topological defect. Topological defects are the subject of almost all my own research up to the present day. The project I am funded by at Keio University is actually called “Topological Science”.

Low-dimensional order

We are almost ready to talk about the Nobel Prize, there is one more piece of historical context necessary. Looking at the first picture, one would guess that ordered phases can exist in a two-dimensional plane as is drawn there, just as it would in real three-dimensional material. Even arrows that live on a line (one-dimensional) could all point in the same direction and be ordered.

Systems with dimension lower than three (so lines and planes) are called low dimensional. Even though everything in reality is three dimensional, one could imagine sheets of matter of one atom layer thick. In physics, even systems of several or several tens or hundreds atoms thick are said to be quasi two-dimensional, which means that they can be very well described by a two-dimensional model. Another important case is the interface between two materials.

So from the early days physicists have wondered about the properties of such low-dimensional systems, with surprising theoretical results. In the 1930s Rudolf Peierls had calculated that sound waves in a two-dimensional solid would be so violent as to prevent the formation of such a solid at all. Random sound waves are always present due to thermal excitation; it is the random motion of atoms in ordered state, let’s say the Brownian motion in solids. But now it turns out that the sound waves are much more pronounced as the dimension of a material gets lower. In the years 1966-1968 Mermin & Wagner, and Hohenberg wrote several articles that showed that this phenomenon is completely general and holds for any order and any phase of matter. The mathematical argument was so elementary that at the time no one doubted that ordered states are not possible in dimensions lower than three. So at the time every physicist was convinced that it is not even worth looking for any sort of order in two-dimensional systems.

Kosterlitz–Thouless phase transition

Every physicist? No, two brave researchers in Birmingham at the time, Kosterlitz and Thouless (and independently and earlier but less exhaustive Berezhinksii in Moscow) kept wondering about models that look like the first picture. The smart thing they did was not to look at what happens to the order parameter (first picture) itself, but what happens to the vortices (second picture). See, if you combine a winding of 360 degrees (vortex) with one of -360 (antivortex), that is, one clockwise and one counter-clockwise, the total configuration has again zero winding. The perturbance of the order due to a vortex–antivortex pair is therefore limited and local. See this picture:

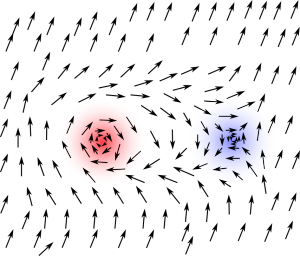
vortex_pair

The arrows at the edge all point in the same direction and, apart from the region in the center, order is maintained. We can now look at the order–disorder phase transition from the point of view of the vortices. This is illustrated by this figure, which features on the cover of my PhD thesis.

vortex_unbinding

The leftmost panel depicts the completely ordered state at low temperature while the rightmost one depicts the the completely disordered state at high temperature. The second panel shows one vortex–antivortex pair which is still a local excitation. The third panel features a few of such pairs. In terms of the arrows, their direction randomizes going left to right, but in terms of the vortices, they become more and more present. This is called vortex unbinding. In the final panel, vortices are no longer bound in pairs with antivortices but can exist freely. Therefore the phase transition from ordered to disordered can be viewed as a vortex-unbinding transition. In physics this is backed up by robust calculations.

The insight of Kosterlitz and Thouless was to start in the disordered state, which must surely be of the unbound vortices type, the rightmost panel. They then asked: what happens to these vortices if one lowers the temperature? And indeed, they found that the vortices at low temperature bind in pairs, even in two dimensions. They explicitly showed there was some ordering phase transition, but the earlier-mentioned theorems precluded the formation of a truly ordered phase. Therefore they discovered, theoretically, a new phase of matter. The interesting thing is that, even though it is surely more ordered than a completely disordered state, it is impossible to find a local order parameter like one can for ordinary phases. Instead, when zooming in the state looks just as in the left panel, but zooming out the direction of the arrows varies greatly. This goes under the name, which you can and should immediately forget, of algebraic long-range order.

The existence of such phases in two-dimensions has now been verified by many calculations and also in several experiments. So this special type of phase, which is neither disordered nor truly ordered, is actually found in nature.

Each type of order has its own type of topological defects, which presumably can undergo a similar unbinding transition. I have looked at this for vortices in superfluids and superconductors, and for topological defects in crystalline order. In the latter case, a solid can disorder into various stages of liquid crystals to finally disorder into a liquid. This is the topic of our most recent paper.

Topological phases

This Nobel Prize awards two more or less separate advances, the first being  the Kosterlitz–Thouless phase transition, and the second what I’ll discuss now. Thouless played an important role here as well, so that half of the Prize has been awarded to him while the other two receive one quarter. This topic concerns an even more obscure concept, topological phases of matter. Since this post has gotten way too long already, I won’t say too much about it.

As before, this is about the characterization of phases of matter that don’t allow for any ordinary order parameter. Instead, there are distinct numbers, like the numbers of holes in a doughnut, that capture global properties of the object as  a whole. The first instance of this is the quantum Hall effect discovered in 1980, which I won’t explain here. Thouless with collaborators showed that this phase of matter can indeed be characterized by a topological number, which does not depend on the local details of the material.

Duncan Haldane is this type of very original thinker that has contributed pioneering ideas to many parts of condensed matter physics. In this case he proposed a model which has surprising properties that would be unbelievable (as they were for quite a while) were it not for robust topological arguments. This model has actually been verified in experiment by now. Furthermore it was the inspiration for a new field of physics that is not even 10 years old, called topological insulators. This is a super-hot topic currently, due to its propensity to be captured by straightforward calculations that can by now be readily put to the test in experiment.

Lorentz chair

On a personal note, the Institute-Lorentz for theoretical physics at Leiden University, where I did my PhD, has an annual visiting professor, called the Lorentz chair, which has boasted many famous names over the years. In the hallway there is a gallery of portraits of Lorentz professors who also, usually subsequently, won the Nobel Prize. I am sure they are very happy to add one more, as Haldane was Lorentz professor in 2008, when I was there. I remember his lectures were both awe-inspiring and rather impenetrable, as they tend to be.

Trieste summer school

Aug 102012
 
 10th August 2012 18:50JST  , , , , ,  3 Responses »

Presently I am at the Abdus Salam International Centre for Theoretical Physics in Trieste, Italy, attending the meeting Innovations in Strongly Correlated Electronic Systems. Amusingly, this first week is a summer school, with extended lectures aimed at providing an introduction or overview of current research topics, whereas next week will be a regular workshop, where scientists present their newest results. The ICTP is a famous place for physics meetings, and they also have researchers and students working here. It is supported by UNESCO, with an explicit mission to support science in developing countries.

The summer school has been very nice so far. It has probably the most international audience I have ever been part of, and from the beginning people have been asking questions abundantly during the presentations. The scope is rather broad, which I like, yet everything is centred around phenomena in materials where the (electron) interactions are strong, as opposed to for instance regular metals and insulators, where the interactions are mostly screened and therefore weak in nature. The most popular compounds are high-temperature superconductors and Mott insulators.

We have live blogging, and video recordings of all the lectures are available online.

Trieste is a great place, at the north-easternmost extremity of Italy, surrounded on three sides by the Slovenian border, on the Adriatic coast. It was the only port of the Habsburg empire, and the previous wealth shows in the many fine buildings in the rather small city. Now it’s mostly tourism, and the centre is filled with restaurants, bars, caffetterie, gelaterie, delicacy shops and so forth. The weather has been excellent so far, between 25 and 30°, and not as humid as Japan. I’m staying in a hotel in the city, which allows for buying some of the exquisite cheeses, meats and bread to take for lunch (superseding the disappointing food served in the canteen here).

update: The workshop was very interesting and successful. For future reference: you can rent a bicycle in Trieste at Surf. My favourite places are Osteria de Scarpon (food) and Osteria da Marino (wine).

Higgs particle

Jul 042012
 
 4th July 2012 16:58JST  , , , , , ,  No Responses »

Today it is/will be announced that the Large Hadron Collider (LHC) accelerator experiment near Geneva has observed the Higgs particle. Although in not my field of expertise, this is a huge discovery in physics, and I will write about it here. Probably some more updates will follow today and later, at the end of this post.

What is the Higgs particle?

Most importantly it is the single missing piece in the puzzle of fundamental particles that is called the Standard Model. This model was developed in the 1960s and on, and makes very precise predictions on which fundamental particles exist, and how they interact. Roughly there are two kinds of partices: matter particles and force particles.

The matter particles comprise quarks (building blocks of protons an neutrons that make up atomic nuclei), electrons and the elusive neutrinos. They all have mass. The force particles cause the matter particles to interact with each other. For instance the electromagnetic force is mediated by light particles, called photons. The force particles are of themselves massless, which is also the reason why photons travel at the maximum velocity, therefore known as the speed of light.

Now it comes: there is yet one other particle, which is unlike all the others. This is the Higgs particle. It does not mediate a force by itself, but instead interacts with the other force particles. When this happens, that force turns from a long-range force to a short-range force. Light does not interact with Higgs, and therefore we can feel a tiny force from stars billions of light years away. The particles that make up the weak nuclear force, responsible for radioactive decay, and unimaginatively called W- and Z-bosons, do interact with Higgs, and therefore only operate within say the atomic nucleus. In physics, this turning into a short-range force is completely equivalent with the force particle “obtaining a mass”, so turning from a massless into a massive particle. This is reason why you can read statement like “Higgs gives mass to all other particles”. The Higgs particle also interacts with some matter particles, but since they are already massive, their mass just gets a little bit bigger.

Bottom line: the fact that the last piece of the puzzle is found is of prime importance, all hyped claims like “God particle” and what not should not be taken seriously.

Interestingly, in precisely the same way as I described above, a magnetic field dies off over a short length in a superconductor, so turns from long-range to short-range. In this context it is called the Anderson-Higgs mechanism, and it is of central importance in my thesis work.

What does an accelerator do?

The big accelerator ring on the Swiss/French border was upgraded some years ago, and was, after an unfortunate accident in 2008, fully operational in 2010. In this ring protons (the nucleus of a hydrogen atom) are accelerated to near light speed in two opposite directions (there are two pipes). At four places these two beams can be made to intersect, such that protons from one beam collide with those from the other.

What happens basically is that two protons combine into a lump of energy, which immediately after splits up into other particles. More precisely, the quarks within the proton do this. They can turn into other quarks, neutrinos, other stuff, and also into the Higgs particle, according to the very precise rules laid out by the Standard model. Those resultant particles then fly away from the collision center and into the detectors. Those are huge instruments to be thought of as the CCD element in your digital camera. They notice when a particle hits them, and can also measure their energy and momentum, like your camera can measure the colour.

However, most of the produced particles including the Higgs are terribly unstable and quickly decay into other particles. So what the detectors measure is not the Higgs particle itself, but remnants of it. Because there is so much going on, so many collisions at the same time, the detectors collect a huge amount of data. This is then processed, first by discarding about 99% of it. The relevant data is analyzed by many people and big computers, and finally interpreted by statistics.

People who’ve ever done something with statistics, know there is always noise. Apart from errors, there are just a lot of random events, for instance particles from space, that your detectors pick up. The real particle collisions add just a few events on top of all of those random ones. So what you have to do is keep measuring and accumulate data, so that the real events start to outnumber the random ones. If there really is a particle that you are interested in, then you look for the predicted collision products with the predicted energy in the predicted directions, and see whether you eventually see a “signal” arising out of the noise.

This signal is compared to computer simulations/calculations based on the Standard Model. These simulations are done beforehand, so people know that if they see a signal, they know to what particular collision process it can be attributed.

In short: you can never see the Higgs particle itself, you can only accumulate evidence that it must have been there.

What has been discovered now?

As mentioned, all particles predicted by the Standard Model have been found except for the Higgs. Therefore the upgrade to the LHC was geared specifically to finding  the Higgs (but also other things are researched). Two experiments, ATLAS and CMS, each and independently look for different collision processes involving the Higgs.

One major problem is that the Standard Model does not predict the mass of the Higgs particle itself (but once you know the mass, the interactions it can undergo are predicted with high precision). Therefore the experiment had to look for all the possibilities that Higgs particles of different mass may incur. This is done by looking for the collision products that should occur. If  with statistical certainty they are not there, then you have “excluded the existence of a Higgs particle with mass x“. Then you do the same for other mass values. In the end you exclude whole mass regions, and this has been done over the past few decades. Of course what you hope for is that the data contradicts the hypothesis that the particle is not there. If that happens with enough certainty, you claim discovery of the particle.

There is a terminology in particle physics, where the “observation” of a particle denotes less certainty than the “discovery” of it. Today they will probably announce “observation of a Higgs particle with mass around 125 GeV”.  Most people are however now convinced that this will not be overturned. This is the greatest physics achievement of this decade, probably of all of science. It is also amazing that a particle predicted in 1964 is now finally confirmed.

What’s next?

First of all, they have to very carefully study the Higgs and check against the Standard Model. There are many properties and interactions, for which there are precise predicitons, to which the Higgs particle should conform. It is not at all certain that this will the case, and there may even be more than one variety of the Higgs particle. Also the Higgs may not be fundamental but consist of other particle itself.

If after all this the conclusion is that there is precisely one variety of Higgs particle which conforms exactly to the Standard Model, and no other particles are found either, then we face a conundrum. Namely, the Standard Model has known problems, it does not explain everything in the world around us. For instance, gravity is not part of it! Search for solutions to these problems is called Beyond the Standard Model physics. The LHC will continue to look for anything that can help answer those questions.

Links

If you have time to spare, you can watch excited nerds talking in an alien language at the CERN live webcast. The best source for physicists is probably Tomasso Dorigo’s live blogging. And don’t believe everything you read and hear in regular media.

Press releases: CERN — NIKHEF

 

I will try to answer questions you may have, in English or Dutch.

Update 5 Jul 11:00JST To be clear about what has been found: both the ATLAS and the CMS experiment see clear evidence with just about enough statistical signficance to claim discovery, for a new, hitherto unobserved particle with a mass of about 126 GeV. The observed behaviour of this particle agrees with what a Standard Model Higgs particle would do, but there is not enough data to unambiguously claim that it is the Higgs. However, we can invoke the duck theorem here: if walks, talks and quacks like a duck, it’s probably a duck.

There is a slight deviation in the so-called two-photon-to-Higgs decay channel, they observe more of those events than one would expect from the number of collisions that have occurred. This may be a statistical fluctuation (the number of events is quite small, just several hundreds), or it may be a real effect that the Standard Model cannot explain. People are hoping for the latter, as it might give a clue in answering the unsolved problems.

 

Nagoya conference on Topological Quantum Phenomena

May 202012
 
 20th May 2012 23:31JST  , , , , ,  No Responses »

From Wednesday up to today I attended the International conference on Topological Quantum Phenomena 2012 in Nagoya. This is one of the meetings held as part of the ministry of education (MEXT) funded five-year program headed by Yoshi Maeno, combining efforts in condensed matter all related by exploring topologically non-trivial states of matter, comprising several research groups in multiple locations in Japan. The plenary talks were presented by Grigori Volovik, Yoichi Ando, Tony Leggett and Shoucheng Zhang, and the scope is indeed rather broad.

Now topological things have always been important ever since Dirac proposed his monopole, but remained usually outside the real mainstream physics. Also, the focus has been mostly on topological defects, which are localized excitations that nevertheless influence the whole system. However, since the discovery of the (fractional) quantum Hall effect, we know that there can also be topological ground states, such that the systems themselves can only be understood by regarding them as a whole, as opposed to having a local order parameter. After so-called topological insulators were predicted and then found a couple of years ago, it seems that topological has become a real buzzword. For me this is interesting, as from my Master’s thesis on I’ve worked on topological stuff.

As pointed out by Volovik already in the first talk, it seems that topology is a necessary ingredient in the general classification scheme of states of matter, which is the principal task of condensed matter physics. So on top of the broken-symmetry paradigm, topological non-trivial aspects need to be taken into account for a full understanding. Moreover, some old knowledge may be better formulated in topology language. According to Volovik, the Fermi surface itself is topologically non-trivial. By the way, his famous book The Universe in a Helium Droplet is very instructive and the draft is freely available.

Overall it was a nice conference with a broad scope that nevertheless seemed to belong to the same endeavour. The scale was quite right with just over 100 people attending on average per day. The interactions during the poster sessions—sometimes a dull affair—were particularly lively. Unfortunately, the deadline for submission was before my arrival in Japan, but I had some interesting discussions anyway.

On Friday there was an excursion to the very large Higashiyama zoo and to Nagoya castle. The latter was destroyed by incendary bombing in 1945, but has been rebuilt in ferroconcrete. Of the cuisinse in particular kochin, a local breed of chicken, was especially good.

Symposium for Akira Tonomura

May 112012
 
 11th May 2012 14:38JST  , , , , , ,  No Responses »

The past two days I attended the Tonomura FIRST International Symposium on “Electron Microscopy and Gauge Fields”, in honor of Akira Tonomura and his efforts in realizing a 1.2 MV electron microscope. Tonomura was the person to first conclusively confirm the Aharonov-Bohm effect, which is one of the wonders of quantum mechanics and one reason why students fall in love with physics (more below).

Incredibly sadly, Tonomura was diagnosed with pancreatic cancer one year ago, seemed to recover well from a major operation, but passed away exactly one week before the symposium. It was supposed to be a grand meeting of his scientific friends, but rather turned into a memorial conference. It was impressive nonetheless, located at the top floor of the Keio hotel with talks by amongst others Yakir Aharonov and Nobel Prize laureats C.N. Yang, Tony Leggett and Makoto Kobayashi. I realized only Wednesday morning that I actually read one of his books, I even cited it in my Master’s thesis.


I particularly liked Aharonov’s talk, in which he explained how he came up with the prediction for the AB-effect. This phenomenon is a variation on the quantum version of Young’s double-slit experiment, which is typically used to verify the wave nature of fields and particles. Here is a cute video portraying the single-electron double-slit experiment. Aharonov and Bohm suggested putting an infinitely thin solenoid right between the slits, so that there is a magnetic field between the trajectories but not on any trajectory the electron can take. In electrodynamics a magnetic field curves the motion of a charged particle (such as an electron), this is called the Lorentz force, but only when the particle actually travels through regions of non-zero magnetic field. AB predict that the interference pattern is shifted from its central position, due to the presence of  a magnetic field in between, even though the electron never  ‘feels’ the magnetic field directly.

In solid state physics, the periodic nature of the atoms or ions in a crystal lattice causes so-called bandgaps in the energy spectrum, which is why some materials are electric insulators and some are metals. The reason behind this is called Bloch’s theorem; so, potentials periodic in space cause gaps in energy. Aharonov told how, as a graduate student, he though about generalizing this to potentials periodic in time, which should analogously lead to gaps in momentum. This was the initial step to the AB effect, which at the time caused a lot of fuss, with some eminent physicists not willing to accept it.

The mechanism behind the AB effect is by now well established and well understood, but it has deep implications for the inherent non-local nature of quantum mechanics. Aharonov proceeded by converting the standard way of looking into the so-called Heisenberg picture, which he claimed identifies much more clearly the non-locality issue. This was very interesting and I’d have to look into this more carefully, perhaps by reading this article or his book.

The second day was devoted to the electron microscopy itself. What people basically do is shoot a beam of electrons at a target sample, and detect the beam a little bit further on. So you’re basically looking at the ‘shadow of the electron beam’, but like with lasers you can also probe phase and coherence properties being altered by the interaction with the sample. The higher the energy you can put in the electron beam, the higher your resolution will be, and by now one can look at individual atoms. There’s a nice explanation on the project’s website itself. On this day I especially enjoyed the talk by David Smith step-by-step outlining the current limits of the machines, and indicating where improvements can be made.

The current project which was initiated and supervised by Tonomura, aims to build a 1.2 MV electron microscope, making it the most powerful in the world. It is expected to be operational next year. It was funded by of the FIRST program, which is basically a part of the money the government assigned to stimulate the economy after the final crisis of 2008. My own group is also funded by this program.

© 2012 Aron Beekman Suffusion theme by Sayontan Sinha